La teoria dei giochi è la scienza matematica che studia e analizza le decisioni individuali di più soggetti che mirano al massimo guadagno personale in base alla scelta che essi compiono. Le decisioni di un individuo possono influire sui risultati conseguibili dagli altri e viceversa, secondo un meccanismo di retroazione, che spinge alla ricerca di soluzioni competitive o cooperative, che in particolare nel contesto economico si riferiscono al caso in cui due o più aziende interagiscono in concorrenza tra loro. Concorrenza perfetta e monopolio rappresentano due forme di mercato estreme. Nel primo caso, nessuno dei partecipanti allo scambio è abbastanza potente (o crede di essere abbastanza potente) da fissare il prezzo di mercato; nel secondo caso, uno degli agenti si trova in una posizione dominante tale da consentirgli di determinare il prezzo. In entrambi i casi, le decisioni prese deriveranno da una previsione del comportamento che adotteranno gli altri soggetti. Per semplificare questa tipologia di problema decisionale, le decisioni di ogni individuo avverranno simultaneamente e indipendentemente dalle decisioni degli altri e senza conoscere la decisione presa dall'altro individuo. Una tale tipologia di problema decisionale prende il nome di gioco. In questo capitolo discutiamo le regole che dovrebbero essere seguite dai partecipanti ad un gioco.
I giochi che prendiamo in considerazione hanno le seguenti caratteristiche. I partecipanti al gioco sono i due individui 1 e 2, ognuno dei quali deve decidere la propria strategia simultaneamente e indipendentemente dalla decisione dell'altro. La vincita (pay-off) di ciascun individuo non dipende solo dalla scelta dell'individuo stesso, ma anche della scelta dell'altro.
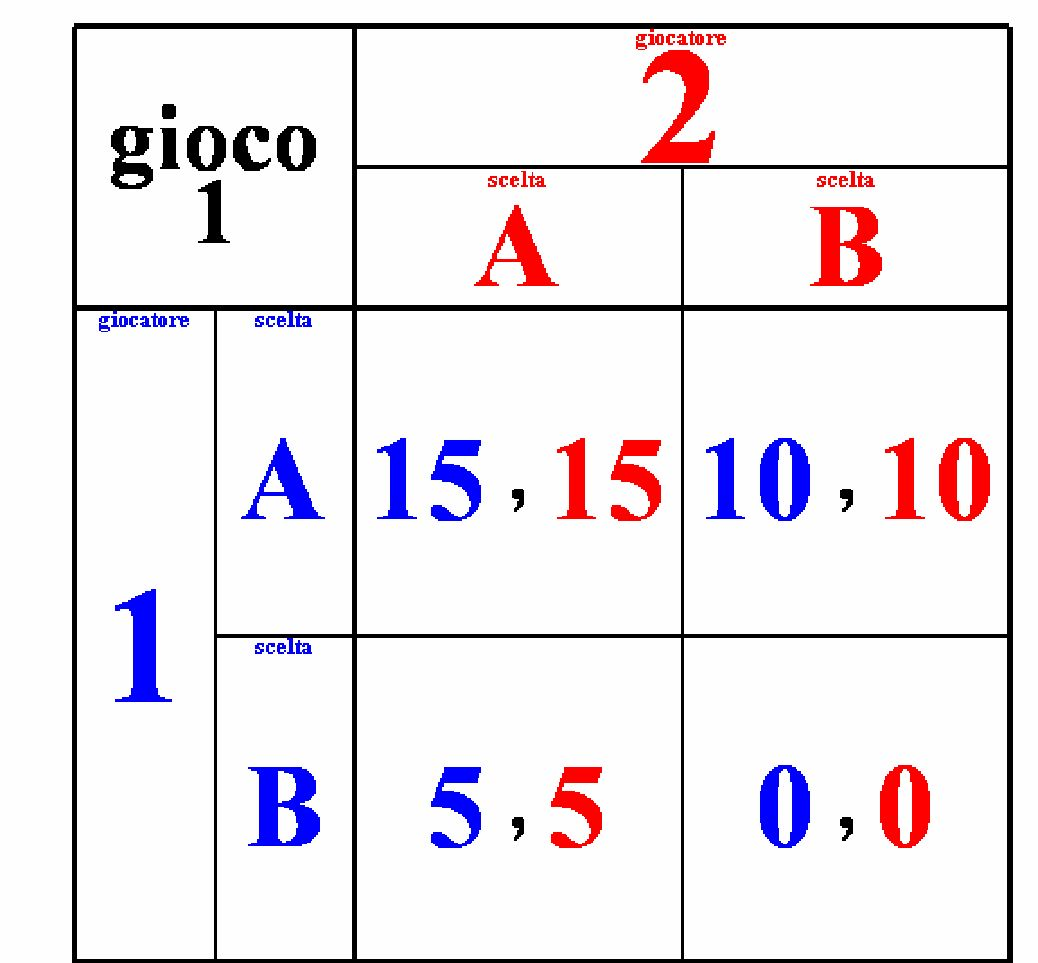
In questo esempio, come in tutti gli altri, chiamiamo l'individuo 1 giocatore di riga, perché deve scegliere di collocarsi in una delle due righe della matrice delle vincite. Analogamente, chiamiamo l'individuo 2 giocatore di colonna, in quanto deve scegliere una delle due colonne della stessa matrice. L'individuo 1 può scegliere tra riga A e riga B. L'individuo 2 può scegliere tra le colonne A e B. Ogni cella della matrice riporta una combinazione alternativa delle vincite dei due giocatori: la prima cifra di ogni combinazione è la vincita dell'individuo 1, la seconda cifra è la vincita dell'individuo 2. E' importante che sia ben chiara la struttura della matrice delle vincite del gioco. Ecco una descrizione dettagliata di tutte le possibili vincite dei due giocatori.
1) Se l'individuo 1 sceglie la riga A e l'individuo 2 sceglie la colonna A, la vincita dell'individuo 1 è 15 e la vincita dell'individuo 2 è 15; 2) Se l'individuo 1 sceglie la riga A e l'individuo 2 sceglie la colonna B, la vincita dell'individuo 1 è 10 e la vincita dell'individuo 2 è 10; 3) Se l'individuo 1 sceglie la riga B e l'individuo 2 sceglie la colonna A, la vincita dell'individuo 1 è 5 e la vincita dell'individuo 2 è 5; 4) Se l'individuo 1 sceglie la riga B e l'individuo 2 sceglie la colonna B, la vincita dell'individuo 1 è 0 e la vincita dell'individuo 2 è 0;
Quali strategie seguono i due giocatori? Ricordiamo che entrambi devono scegliere in maniera simultanea e indipendente: un giocatore decide la strategia da seguire senza conoscere la strategia dell'altro. Come vi comportereste al posto del giocatore 1? La vostra vincita dipende dalla scelta del giocatore 2. Quindi, è logico chiedersi quale sia la strategia preferita dal giocatore 2. Se il giocatore 2 sceglie la colonna A, la vostra strategia preferita è la riga A (15 è una vincita maggiore di 5). Se il giocatore 2 sceglie la colonna B la vostra strategia migliore è scegliere la riga A (10 è una vincita maggiore di 0). Di conseguenza, la migliore strategia del giocatore 1 è scegliere la riga A indipendentemente dalla scelta del giocatore 2: la scelta della riga A è una strategia dominante per il giocatore 1 in quanto comporta la vincita maggiore, qualsiasi sia la strategia seguita dal giocatore 2. Cosa possiamo dire del giocatore 2? Il secondo giocatore ha una strategia dominante? Nel nostro esempio la risposta è "si". Se il giocatore 1 sceglie la riga A, la strategia migliore per 2 è scegliere la colonna A (15 è maggiore di 10). Se il giocatore 1 sceglie la riga B, la strategia migliore per 2 è scegliere la colonna A (5 è maggiore di 0). Anche il giocatore 2 ha una strategia dominante nel gioco: scegliere la colonna A. Il risultato del gioco è facilmente prevedibile: l'individuo 1 sceglie la riga A (la sua strategia dominante) e l'individuo 2 sceglie la colonna A (la sua strategia dominante). Il risultato del gioco è (A, A) e ogni giocatore riceve una vincita di 15.
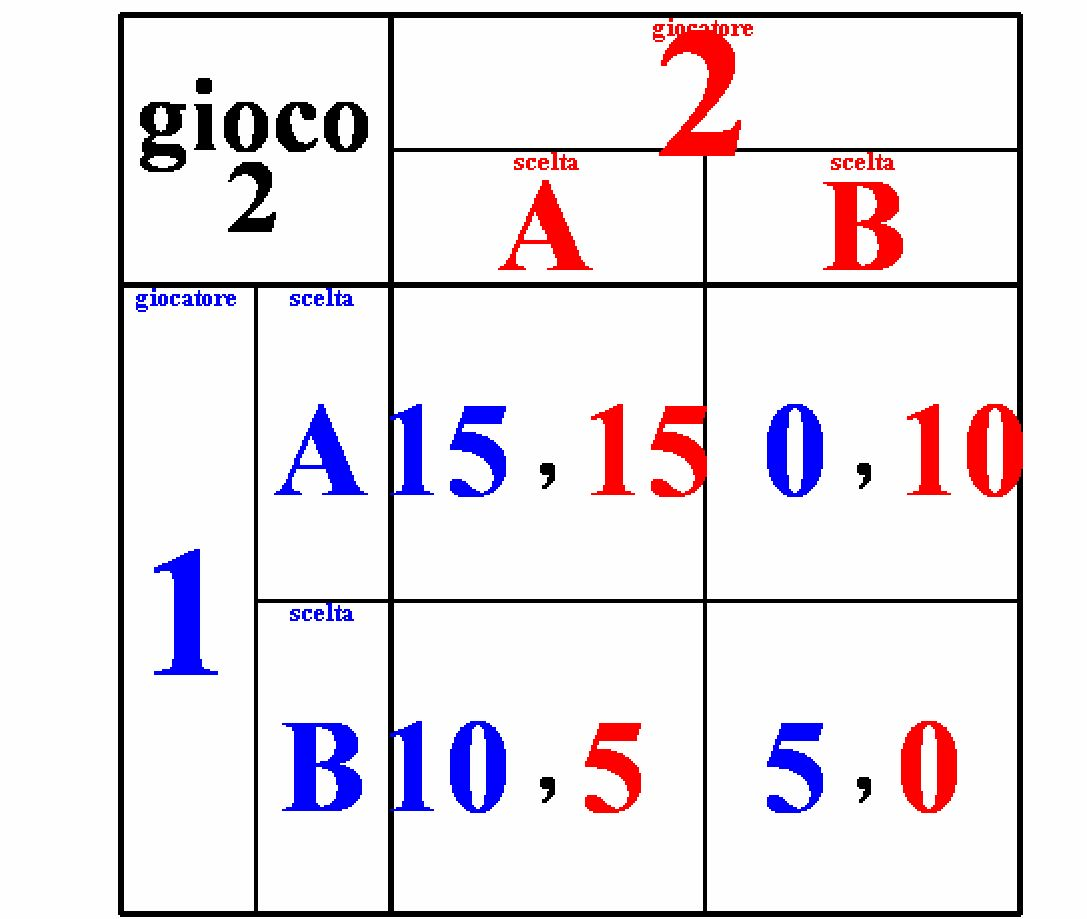
Non tutti i giochi sono semplici come quello illustrato nell'esempio precedente. Analizziamo il gioco 2, al quale è associato la matrice delle vincite della tabella 30.2. I giocatori hanno una strategia dominante? Verifichiamolo a partire dal giocatore 1.
1) se il giocatore 2 sceglie la colonna A, la strategia migliore per il giocatore 1 è scegliere la riga A; 2) se il giocatore 2 sceglie la colonna B, la strategia migliore per il giocatore 1 è scegliere la riga B.
Il giocatore 1 non ha una strategia dominante. E il giocatore 2?
1) se il giocatore 1 sceglie la riga A, la strategia migliore per il giocatore 2 è scegliere la colonna A; 2) se il giocatore 1 sceglie la riga B, la strategia migliore per il giocatore 2 è scegliere la colonna A.
Il giocatore 2 ha una strategia dominante: scegliere la colonna A. E' questa la strategia che implica la vincita più elevata per il giocatore 2, qualsiasi strategia scelga di seguire il giocatore 1.
Pur in assenza di una strategia dominante, il giocatore 1 potrebbe essere in grado di prevedere che il giocatore 2 ha una strategia dominante (scegliere la colonna A). In base a questa informazione si può svolgere il seguente ragionamento. Se il giocatore 2 sceglie la colonna A, la migliore strategia del giocatore 1 è scegliere la riga A. Di conseguenza, il giocatore 2 sceglie la colonna A e il giocatore 1, conoscendo la scelta del giocatore 2, sceglie la riga A. Il gioco ha per risultato la combinazione di vincite (A, A) ed entrambi i giocatori guadagnano 15. Tale risultato soddisfa entrambi i giocatori. Infatti, per nessuno dei due è conveniente cambiare la propria decisione. E' importante notare che ciò non è vero per tutti gli altri possibili risultati del gioco: in (A,B) il giocatore 2 preferisce cambiare scelta; il giocatore 1 preferisce spostarsi da (B,A); in (B,B) il giocatore 2 preferisce cambiare scelta. Questa proprietà, conferisce alla combinazione (A,A) la definizione di Equilibrio di Nash: a nessuno dei due giocatori conviene cambiare strategia data la scelta dell'altro giocatore. Tutti i giochi sono caratterizzati dalla presenza di un Equilibrio di Nash?
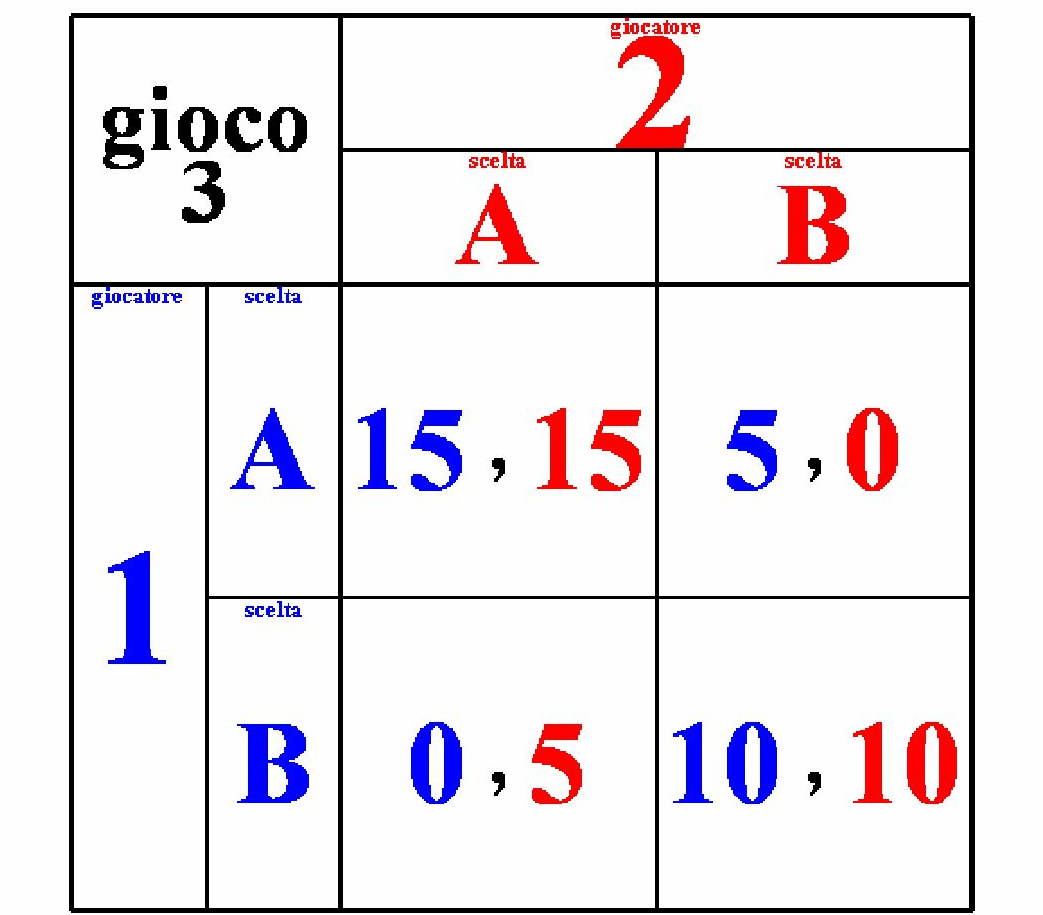
Il gioco 3 ha due Equilibri di Nash: (A,A) e (B,B). Si potrebbe dire che nella realtà sia più probabile che il gioco abbia per risultato (A,A), ma cosa accadrebbe se le vincite di "5" fossero sostituite da due perdite? Se è certo che il giocatore 2 sceglie la colonna A, il giocatore 1 non ha nessun problema. Ma se pensa che il giocatore 2 possa scegliere la colonna B, scegliere la riga B diventa la strategia meno rischiosa perché elimina la probabilità di subire una perdita. (A, A) è un Equilibrio di Nash perché al giocatore 1 non conviene cambiare la propria scelta della riga A se il giocatore 2 ha scelto la colonna A e al giocatore 2 non conviene cambiare la propria scelta della colonna A se il giocatore 1 ha scelto la riga A. Anche (B, B) è un Equilibrio di Nash perché al giocatore 1 non conviene spostarsi dalla riga B se il giocatore 2 ha scelto la colonna B e al giocatore 2 non conviene spostarsi dalla colonna B se il giocatore 1 ha scelto la riga B.
E' possibile che un gioco non abbia nessun Equilibrio di Nash.
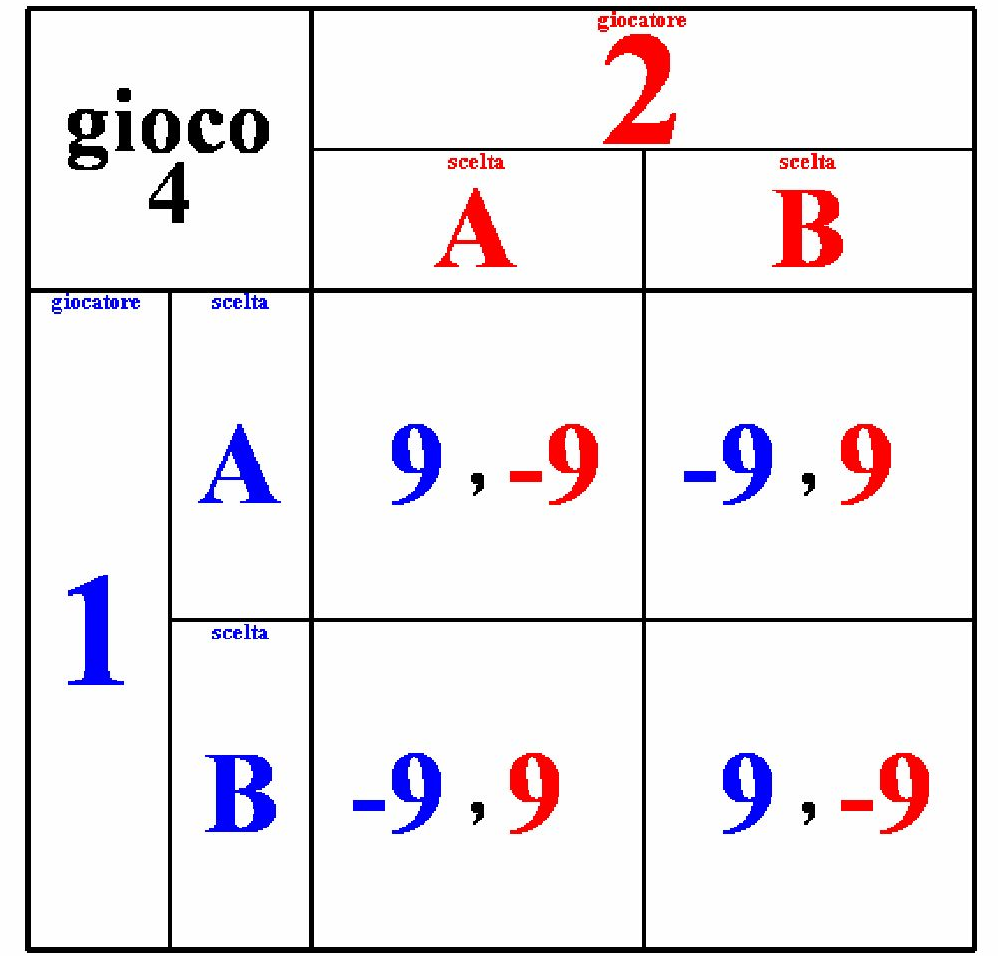Le combinazioni delle vincite dei due giocatori del gioco 4 sono le seguenti:
1) (A, A) non è un Equilibrio di Nash: al giocatore 2 conviene cambiare strategia; 2) (A, B) non è un Equilibrio di Nash: al giocatore 1 conviene cambiare strategia; 3) (B, A) non è un Equilibrio di Nash: al giocatore 1 conviene cambiare strategia; 4) (B, B) non è un Equilibrio di Nash: al giocatore 2 conviene cambiare strategia.
Per questa tipologia di giochi, è necessario estendere il concetto di Equilibrio di Nash e considerare strategie più complesse. Quale pensate sia la migliore strategia di un giocatore? Ovviamente una strategia che confonda l'altro giocatore in quanto se l'altro è a conoscenza della nostra scelta può sfruttare a proprio vantaggio questa informazione. E qual è il modo migliore per confondere l'altro giocatore? Scegliere A o B casualmente e con la stessa probabilità. Questa strategia è conosciuta con il nome di strategia mista. Il gioco 4 ha un equilibrio con strategie miste.
Analizziamo nel dettaglio le proprietà di questo altro gioco famoso: il dilemma del prigioniero.
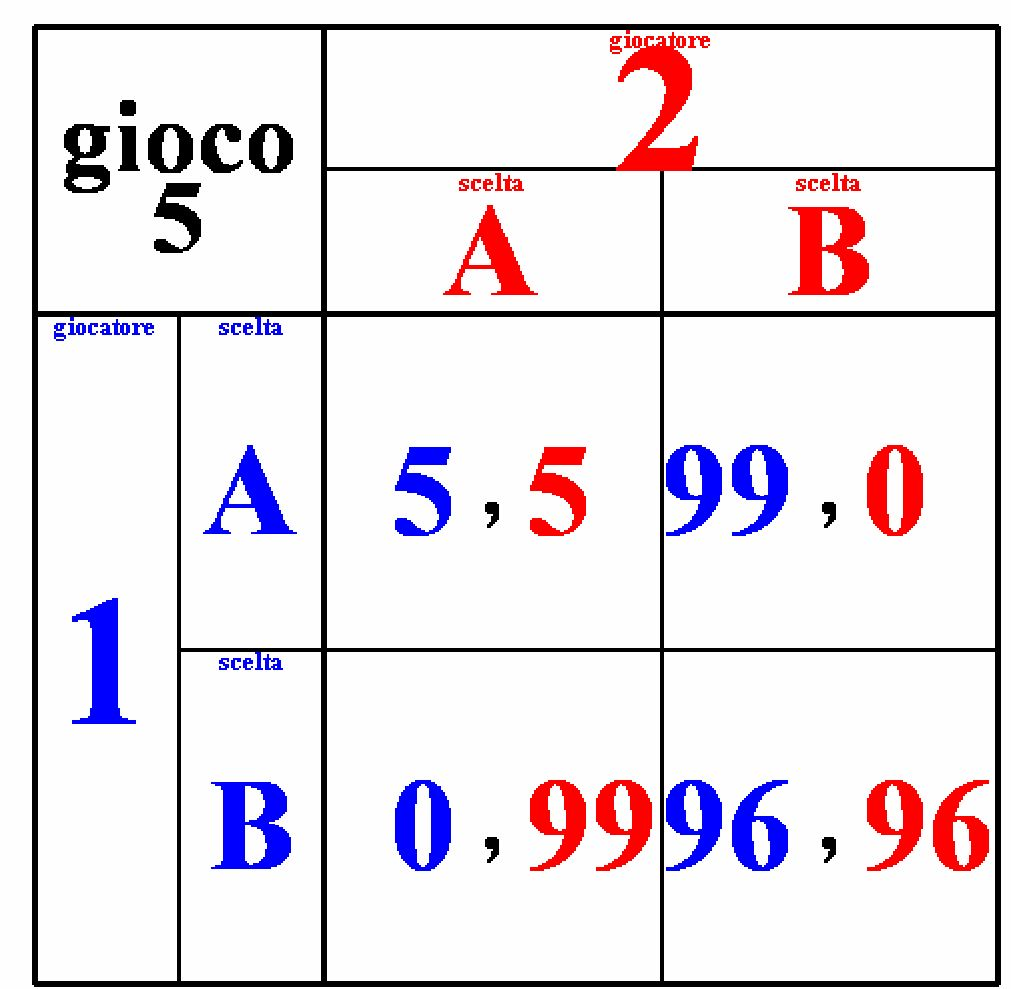
Si tratta di un gioco simmetrico (ma non deve esserlo necessariamente), vale a dire che è sufficiente osservare le mosse di uno solo dei due giocatori. Consideriamo il giocatore 1: data la colonna A, la vincita del giocatore 1 è maggiore nella riga A che nella riga B. Data la colonna B, la vincita del giocatore 1 è maggiore nella riga A che nella riga B. Inoltre e più importante, la vincita del giocatore 1 è maggiore in (B, B) che in (A, A). Data la simmetria del gioco, ciò implica che l'esito (B, B) domina l'esito (A, e A). In altri termini, entrambi i giocatori preferiscono (B, B) ad (A, A). Ricordate questo risultato. Ma qual è la nostra previsione? Verificando l'esistenza di una strategia dominante per uno dei due giocatori, concludiamo che ne hanno una entrambi. Il giocatore 1 preferisce scegliere la riga A indipendentemente dalla strategia del giocatore 2; il giocatore 2 preferisce collocarsi nella colonna A indipendentemente dalla strategia del giocatore 1. La previsione che il giocatore 1 scelga la riga A e il giocatore 2 scelga la colonna A (sono queste le loro rispettive strategie dominanti) porta alla conclusione che la coppia di vincite per questo gioco sarà inevitabilmente (A, A). E' questo l'unico equilibrio di Nash del gioco. L'esito (A, A) è dominato da (B, B). Ma nonostante questa proprietà, (B, B) non è un Equilibrio di Nash. Infatti, ad entrambi giocatori converrebbe spostarsi da (B, B). Nel nostro esempio sia 1 che 2 preferiscono A.
Estendiamo dunque i concetti esposti nei paragrafi precedenti ad un problema di scelta nel continuo. Chiamiamo la variabile di scelta q e i due individui che prendono parte al gioco giocatore 1 e giocatore 2. Chiamiamo q1 la scelta del giocatore 1 e q2 la scelta del giocatore 2. Il caso in cui entrambi i giocatori hanno una strategia dominante è di facile comprensione. In tal caso, infatti, la strategia ottima di ciascun giocatore non dipende dalla decisione dell'altro. Il grafico contiene due rette. Esse rappresentano la relazione tra la scelta ottima di un giocatore e la scelta ottima dell'altro. In due giocatori hanno entrambi una strategia dominante e, di conseguenza, la scelta ottima del giocatore 1 in funzione della scelta ottima del secondo giocatore è una retta verticale (orizzontale).
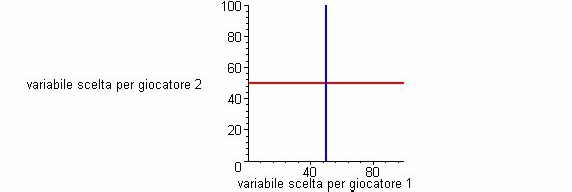
La scelta ottima del giocatore 1 è 50, qualunque sia la scelta del giocatore 2. La sua strategia dominante è quindi scegliere 50 indipendentemente dalla strategia del giocatore 2. La scelta ottima del giocatore 2 qualunque sia la scelta del giocatore 1. La sua strategia dominante è scegliere 50 indipendentemente dalla strategia del giocatore 1. L'esito di questo gioco si colloca in corrispondenza dell'intersezione delle due rette, per cui entrambi i giocatori scelgono 50. A questo punto è necessario introdurre un po' di terminologia. La relazione che definisce la scelta ottima di un giocatore in funzione della scelta ottima dell'altro giocatore è conosciuta con il nome di funzione di reazione. La retta verticale è la funzione di reazione del giocatore 1 e la retta orizzontale è la funzione di reazione del giocatore 2. E' importante sottolineare che tale terminologia può essere forviante perché suggerisce che i giocatori reagiscano alla mossa dell'altro, il che non è possibile in un gioco simultaneo. Dunque, è bene ricordare che la funzione di reazione di un giocatore ha semplicemente lo scopo di esprimere la scelta ottima di un giocatore in funzione della scelta ottima dell'altro. Possiamo usare le funzioni di reazione per dimostrare l'esistenza dell'equilibrio di Nash. Ricordiamo che nell'Equilibrio di Nash nessuno dei due giocatori trova conveniente cambiare strategia data la scelta dell'altro. E' facile intuire che ogni Equilibrio di Nash deve collocarsi nel punto di intersezione delle due funzioni di reazione.
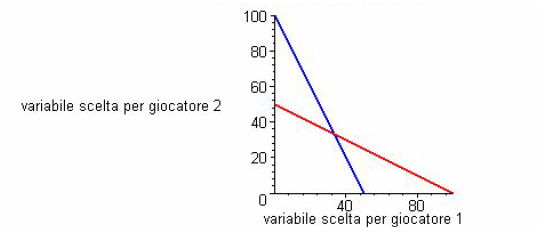
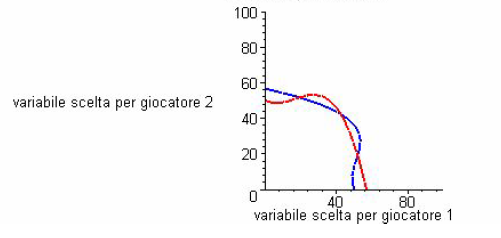
Le due funzioni di reazione si intersecano in un punto: l'unico Equilibrio di Nash del gioco. In ogni punto al di fuori delle rispettive funzioni di reazione, i due giocatori trovano conveniente riconsiderare la propria decisione. Solo quando i due giocatori si trovano simultaneamente lungo le rispettive funzioni di reazione, il gioco ha un esito tale che a nessuno dei due conviene cambiare scelta. Naturalmente è possibile che un gioco abbia 2 Equilibri di Nash.
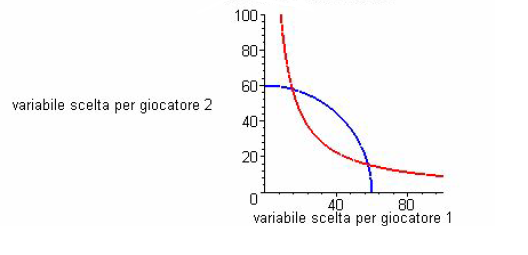
Un gioco può avere anche 3 o più Equilibri di Nash.
These are some elements of the game theory. These are simultaneous games with 2 players, where each player must choose his strategy without knowing what the other one chose. Games with dominant strategy are easy to solve. A player has dominant strategy if this strategy is optimal independently of the strategy chose by the other player. Other games can be more complicated and Nash equilibrium can be very useful for their solution. The result of a game is a Nash equilibrium when the change of choice isn't conveniente for any player. A game can have: no Nash equilibrium, one Nash equilibrium or multiple Nash equilibrium. Those concepts are important in games with only two possibility of choice and in games where the choice takes place in the continuous. For this type of games we have defined the concept of the player's reaction function. This function defines the best choice of a player depending of the other player's choice function.